エマオ塾浜ノ宮教室の二階は標高約50m。窓から海がよく見える。晴れた日には遠くまで。水平線を船が行く。何キロ先にいるのだろう?
「わぁ、綺麗!」「いい景色!」
「水平線が遠いよね、さっき海岸で見た時より」
はい、ちょっと計算してみましょう、目の高さとそこから見える水平線までの距離の関係。三平方の定理を使います。
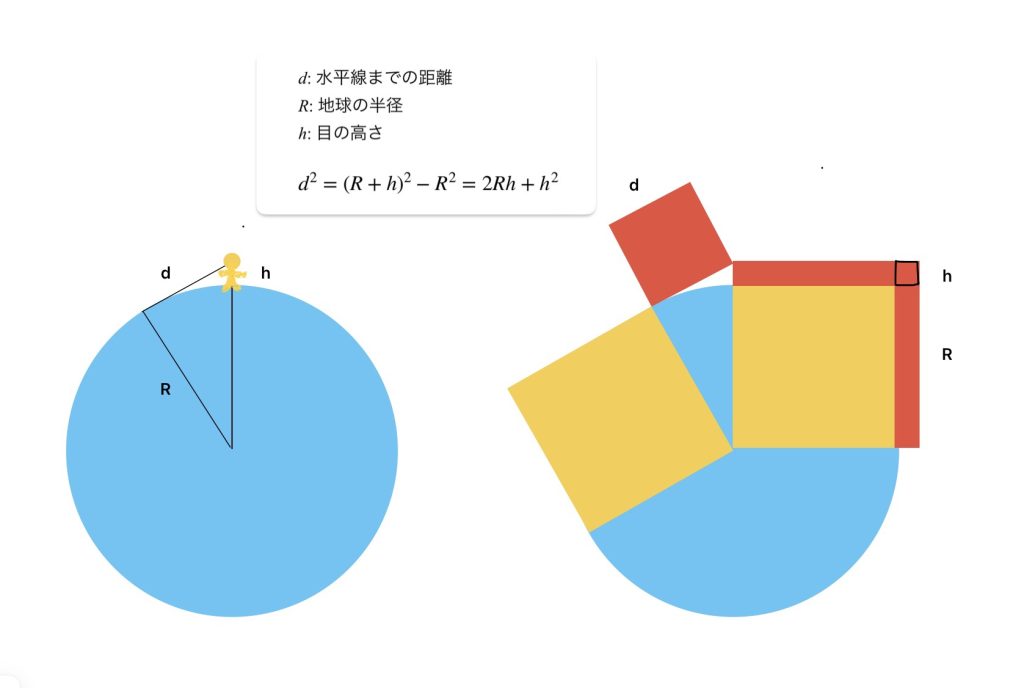
つまり、水平線までの距離の二乗は、地球の直径かける目の高さ プラス 目の高さの二乗。ここで目の高さが地球の直径と比べてずっと小さい時は、目の高さの二乗はずっとずっと小さいので無視してよくて、水平線までの距離の二乗はだいたい地球の直径かける目の高さ、となります。
例えば、海岸に立っている時の目の高さを1.5mとすると、地球の直径は約12,800kmつまり約12,800,000mなので、水平線までの距離の二乗は約12,800,000mかける1.5m、すなわち約19,200,000㎡となります。水平線までの距離はこれの平方根なので、電卓、電卓! この√というキーを押して、はい、4,381.78046っと。約4.4km。海岸に立っていた時は4、5キロ先まで見えていたんですね。
ここからはどうでしょう?目の高さを50mとして同じように計算してみましょう。
12,800,000かける50、の平方根、ですね。はい、電卓で。出ましたか?
25,298.2213
25キロくらいですね。うん、結構遠くまで見えてるんだねぇ。
じゃあ、富士山のてっぺんからならどうだろう?富士山は高さ3,776mね。どこまで見えるかな?逆に言うと、どのくらい遠くから富士山のてっぺん見えるかな?さあ、やってみよう!